TAVOLE 14-15-16 A3(17-18-19 A4) Proiezioni ortogonali
Tavola 17 in formato A4 orizzontale, in sostituzione della tavola 14 formato A3
Tavola 19 in formato A4 orizzontale, in sostituzione della tavola 16 formato A3
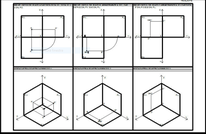
TAVOLA 14 A3 Proiezioni ortogonali di punti
1. Proiezione Ortogonale del punto A. Distanza dal P.O.18; Distanza dal P.V.30; Distanza dal P.L.25
2. Assonometria Isometrica del punto A.
3. Proiezione Ortogonale del punto B appartenente al P.O. Distanza dal P.O. 0; Distanza dal P.V.32; Distanza dal P.L.40
4. Assonometria Isometrica del punto B.
5. Proiezione Ortogonale del punto C. appartenente al P.V. Distanza dal P.O. 37; Distanza dal P.V. 0; Distanza dal P.L. 28.
6. Assonometria Isometrica del punto C.
Es. 1
1. Disporre i 3 piani P.O., P.V. e P.L. tra di loro perpendicolari. L’asse z separa il P.V. dal P.L.;l’asse x separa il P.O. dal P.V. e corrisponde alla Linea Terra; l’asse y delimita il P.L. e il P.O. I 3 assi si intersecano nell’origine O.
2. Per calcolare la distanza dal P.O. misurare 18mm sull’asse z, allontanandosi dall’origine O verso l’alto.
3. Per calcolare la distanza dal P.L. spostarsi sull’asse x di 25mm a partire dall’origine O, verso sinistra.
4. Per calcolare la distanza dal P.V. misurare 30mm sull’asse y, allontanandosi dall’origine O verso il basso. Oppure misurare 30mm sull’asse y allontanandosi dall’origine O verso destra.
5. Con segno di costruzione far passare le parallele agli assi x,y,e z per i punti trovati nei tre passaggi precedenti.
6. Queste parallele si intersecano nei punti A’, A’’ e A’’’ rispettivamente proiezione sul P.V., proiezione sul P.O. e proiezione sul P.L.
Es. 2
1. Disporre i 3 assi x, y e z in modo che formino 3 angoli da 120°. (Un angolo di 120° si può costruire con un angolo di 90° sommato ad un angolo di 30°).
2. Riportare lungo l’asse z, a partire da O proseguendo verso l’alto, la misura di 18mm (distanza dal P.O.).
3. Riportare lungo l’asse y, a partire da O proseguendo inclinati di 30° verso il basso a destra, la misura di 30mm (distanza dal P.V.).
4. Riportare lungo l’asse x, a partire da O proseguendo inclinati di 30° verso il basso a sinistra, la misura di 25mm (distanza dal P.L.).
5. Far passare per ognuno di questi 3 punti, con segno di costruzione, le parallele agli assi x,y, e z.
6. Queste parallele si intersecano nei punti A’ proiezione sul P.V., A’’ proiezione sul P.O.,e A’’’ proiezione sul P.L.
7. Per trovare il punto reale A, tracciare le parallele agli assi x,y e z passanti per i punti A’, A’’ e A’’’.
Queste parallele si intersecano nel punto reale A.
Es.3
1. Disporre i 3 piani P.O., P.V. e P.L. tra di loro perpendicolari. L’asse z separa il P.V. dal P.L.;l’asse x separa il P.O. dal P.V. e corrisponde alla Linea Terra; l’asse y delimita il P.L. e il P.O. I 3 assi si intersecano nell’origine O.
2. Non è necessario calcolare la distanza dal P. O. poiché giace sul P. O., quindi la distanza è 0.
3. Per calcolare la distanza dal P.L. spostarsi sull’asse x di 40mm a partire dall’origine O, verso sinistra, trovando così il punto B’.
4. Per calcolare la distanza dal P.V. misurare 32mm sull’asse y, allontanandosi dall’origine O verso il basso, trovando così il punto B’’’. Oppure misurare 30mm sull’asse y allontanandosi dall’origine O verso destra.
5. Con segno di costruzione far passare le parallele agli assi x e y per i punti trovati nei due passaggi precedenti.
6. Queste parallele si intersecano nel punto B≡B’’sul P.O, perché il punto reale B coincide con la sua proiezione sul P.O.
Es.4
1. Disporre i 3 assi x, y e z in modo che formino 3 angoli da 120°. (Un angolo di 120° si può costruire con un angolo di 90° sommato ad un angolo di 30°).
2. Riportare lungo l’asse y verso destra, a partire da O, la misura di 32mm (distanza dal P.V.).
3. Riportare lungo l’asse x verso sinistra, a partire da O, la misura di 40mm (distanza dal P.L.).
4. Far passare per ognuno di questi 2 punti, con segno di costruzione, le parallele agli assi x e y.
5. Queste parallele si intersecano nel punto B≡ B’’ sul P.O., perché il punto reale B coincide con la sua proiezione sul P.O.
Es.5
1. Disporre i 3 piani P.O., P.V. e P.L. tra di loro perpendicolari. L’asse z separa il P.V. dal P.L.;l’asse x separa il P.O. dal P.V. e corrisponde alla Linea Terra; l’asse y delimita il P.L. e il P.O. I 3 assi si intersecano nell’origine O.
2. Non è necessario calcolare la distanza dal P. V. poiché giace sul P. V., quindi la distanza è 0.
3. Per calcolare la distanza dal P.L. spostarsi sull’asse x di 28mm a partire dall’origine O, verso sinistra, trovando così il punto C’’.
4. Per calcolare la distanza dal P.O. misurare 37mm sull’asse z, allontanandosi dall’origine O verso l’alto, trovando così il punto C’’’.
5. Con segno di costruzione far passare le parallele agli assi x e z per i punti trovati nei due passaggi precedenti.
6. Queste parallele si intersecano nel punto C≡C’sul P.V, perché il punto reale C coincide con la sua proiezione sul P.V.
Es.6
1. Disporre i 3 assi x, y e z in modo che formino 3 angoli da 120°. (Un angolo di 120° si può costruire con un angolo di 90° sommato ad un angolo di 30°).
1. Riportare lungo l’asse z verso l’alto, a partire da O, la misura di 37mm (distanza dal P.O.).
2. Riportare lungo l’asse x verso sinistra, a partire da O, la misura di 28mm (distanza dal P.L.).
3. Far passare per ognuno di questi 2 punti, con segno di costruzione, le parallele agli assi x e z.
4. Queste parallele si intersecano nel punto C≡ C’ sul P.V., perché il punto reale C coincide con la sua proiezione sul P.V.
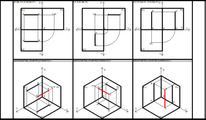
TAVOLA 15 A3 Proiezioni ortogonali di segmenti
1. Proiezione Ortogonale del segmento AB(32) perpendicolare al P.L. e parallelo al P.O. e al P.V. L’estremo B dista 10 dal P.L., 35 dal P.O. e 28 dal P.V.
2. Assonometria Isometrica del segmento AB.
3. Proiezione Ortogonale del segmento CD (28)perpendicolare al P.V. e parallelo al P.L. e al P.O.
L’estremo C dista 10 dal P.V., 35 dal P.O. e 20 dal P.L.
4. Assonometria Isometrica del segmento CD.
5. Proiezione Ortogonale del segmento EF (42) perpendicolare al P.O. e parallelo agli altri due. L’estremo F dista 0 dal P.O., 25 dal P.L. e 30 dal P.V.
6. Assonometria Isometrica del segmento EF.
Es. 1
1. Disporre i 3 piani P.O., P.V. e P.L. tra di loro perpendicolari. L’asse z separa il P.V. dal P.L.;l’asse x separa il P.O. dal P.V. e corrisponde alla Linea Terra; l’asse y delimita il P.L. e il P.O. I 3 assi si intersecano nell’origine O.
2. Per calcolare la distanza del punto B dal P.O. misurare 35mm sull’asse z, allontanandosi dall’origine O verso l’alto.
3. Per calcolare la distanza del punto B dal P.L. spostarsi sull’asse x di 10mm a partire dall’origine O, verso sinistra.
4. Per calcolare la distanza del punto B dal P.V. misurare 28mm sull’asse y, allontanandosi dall’origine O verso il basso. Oppure misurare 28mm sull’asse y allontanandosi dall’origine O verso destra. Oppure, trovato B’’, arrivare fino all’asse y del Piano Orizzontale con una linea di riferimento; puntare il compasso in O e trasportare questa distanza sull’asse y del Piano Laterale.
5. Con segno di costruzione far passare le parallele agli assi x,y,e z per i punti trovati nei tre passaggi precedenti.
6. Queste parallele si intersecano nei punti B’, B’’ e B’’’ rispettivamente proiezione sul P.V., proiezione sul P.O. e proiezione sul P.L.
7. A partire dalla proiezione B’ sul P.V. riportare il segmento A’B’=32 verso sinistra e parallelamente alla Linea Terra.
8. Far scendere dal punto A’ la proiettante, o linea di riferimento, perpendicolare all’asse x e proseguire fino ad incontrare il prolungamento della proiettante da B’’, individuando così il punto A’’.
9. Evidenziare i segmenti A’B’, proiezione sul P.V, e A’’B’’, proiezione sul P.O. Lasciare le linee di riferimento in linea di costruzione.
10. La proiezione del segmento sul P.L. si riduce ad un punto poiché la proiezione dell’estremo A’’’ coincide con l’estremo B’’’. Si ricorda che si deve scrivere prima la lettera A’’’ e poi B’’’ perché si deve seguire l’ordine di lettura dal punto di osservazione del segmento (in questo caso da sinistra verso destra).
Es. 2
1. Disporre i 3 assi x, y e z in modo che formino 3 angoli da 120°. (Un angolo di 120° si può costruire con un angolo di 90° sommato ad un angolo di 30°).
2. Riportare lungo l’asse z, a partire da O proseguendo verso l’alto, la misura di 35mm (distanza del punto B dal P.O.).
3. Riportare lungo l’asse y, a partire da O proseguendo inclinati di 30° verso il basso a destra, la misura di 28mm (distanza dal P.V.).
4. Riportare lungo l’asse x, a partire da O proseguendo inclinati di 30° verso il basso a sinistra, la misura di 10mm (distanza dal P.L.).
5. Far passare per ognuno di questi 3 punti, con segno di costruzione, le parallele agli assi x,y, e z.
6. Queste parallele si intersecano nei punti B’, proiezione sul P.V., B’’ proiezione sul P.O.,e B’’’ proiezione sul P.L.
7. Per trovare il punto reale B, tracciare le parallele agli assi x,y e z passanti per i punti B’, B’’ e B’’’.
Queste parallele si intersecano nel punto reale B.
8. Per trovare il punto reale A, secondo estremo del segmento, prolungare la parallela all’asse x, a partire dal punto B’, verso il basso a sinistra, restando sempre inclinati di 30°, di un lunghezza pari al segmento, cioè 32 mm. Si individua così il punto A’.
9. Da A’ e B’ si scende perpendicolarmente, paralleli all’asse z, fino ad incontrare la Linea Terra. Dalla Linea Terra si può proseguire parallelamente all’asse y fino ad incontrare il prolungamento che parte dal punto B’’.
10. E cioè: dal punto B’’ si procede parallelamente all’asse x verso il basso a sinistra sempre di 32mm, fino ad individuare il punto A’’.
11. Per trovare il punto reale A, tracciare le parallele agli assi y e z passanti per i punti A’e A’’.
Queste parallele si intersecano nel punto reale A.
12. Il punto A è il secondo estremo del segmento AB. Si consiglia di evidenziare il segmento reale AB con un colore diverso per distinguerlo dalle sue proiezioni.
Es.3
1. Disporre i 3 piani P.O., P.V. e P.L. tra di loro perpendicolari. L’asse z separa il P.V. dal P.L.;l’asse x separa il P.O. dal P.V. e corrisponde alla Linea Terra; l’asse y delimita il P.L. e il P.O. I 3 assi si intersecano nell’origine O.
2. Per calcolare la distanza del punto C dal P.O. misurare 35mm sull’asse z, allontanandosi dall’origine O verso l’alto.
3. Per calcolare la distanza del punto C dal P.L. spostarsi sull’asse x di 20mm a partire dall’origine O, verso sinistra.
4. Per calcolare la distanza del punto C dal P.V. misurare 10mm sull’asse y, allontanandosi dall’origine O verso il basso. Oppure misurare 10mm sull’asse y allontanandosi dall’origine O verso destra.
5. Con segno di costruzione far passare le parallele agli assi x,y,e z per i punti trovati nei tre passaggi precedenti.
6. Queste parallele si intersecano nei punti C’, C’’ e C’’’ rispettivamente proiezione sul P.V., proiezione sul P.O. e proiezione sul P.L.
7. A partire dal punto C’’ sul P.O. riportare il segmento C’’D’’=28 verso il basso e parallelamente all’asse y. Si individua così il punto D’’.
8. Far partire dai punto C’’ e D’’ le linee di riferimento parallele all’asse x, fino ad incontrare l’asse y del Piano Orizzontale. Puntare il compasso in O e portare queste due misure sull’asse y del Piano Laterale.
9. Da qui proseguire verticalmente, paralleli all’asse z, fino ad incontrare la linea di riferimento che da C’ prosegue parallelamente all’asse x. Si individuano così i punti C’’’ e D’’’.
10. Evidenziare i segmenti C’’D’’, proiezione sul P.O, e C’’’D’’’, proiezione sul P.L. Lasciare le linee di riferimento in linea di costruzione.
11. La proiezione del segmento sul P.V. si riduce ad un punto poiché la proiezione dell’estremo D’ coincide con l’estremo C’. Si ricorda che si deve scrivere prima la lettera D’ e poi C’ perché si deve seguire l’ordine di lettura dal punto di osservazione del segmento (in questo caso dal basso verso l’alto).
Es.4
1. Disporre i 3 assi x, y e z in modo che formino 3 angoli da 120°. (Un angolo di 120° si può costruire con un angolo di 90° sommato ad un angolo di 30°).
2. Riportare lungo l’asse z, a partire da O proseguendo verso l’alto, la misura di 35mm (distanza del punto C dal P.O.).
3. Riportare lungo l’asse y, a partire da O proseguendo inclinati di 30° verso il basso a destra, la misura di 10mm (distanza dal P.V.).
4. Riportare lungo l’asse x, a partire da O proseguendo inclinati di 30° verso il basso a sinistra, la misura di 20mm (distanza dal P.L.).
5. Far passare per ognuno di questi 3 punti, con segno di costruzione, le parallele agli assi x,y, e z.
6. Queste parallele si intersecano nei punti C’, proiezione sul P.V., C’’ proiezione sul P.O.,e C’’’ proiezione sul P.L.
7. Per trovare il punto reale C, tracciare le parallele agli assi x,y e z passanti per i punti C’, C’’ e C’’’.
Queste parallele si intersecano nel punto reale C.
8. Per trovare il punto reale D, secondo estremo del segmento, prolungare la parallela all’asse y, a partire dal punto C’’’, verso il basso a destra, restando sempre inclinati di 30°, di un lunghezza pari al segmento, cioè 28 mm. Si individua così il punto D’’’.
9. Da C’’’ e D’’’ si scende perpendicolarmente, paralleli all’asse z, fino ad incontrare l’asse y. Dall’asse y si può proseguire parallelamente all’asse x fino ad incontrare il prolungamento che parte dal punto C’’.
10. E cioè: dal punto C’’ si procede parallelamente all’asse y verso il basso a destra sempre di 28mm, fino ad individuare il punto D’’.
11. Per trovare il punto reale D, tracciare le parallele agli assi z e x passanti per i punti D’’e D’’’.
Queste parallele si intersecano nel punto reale D.
12. Il punto D è il secondo estremo del segmento CD. Si consiglia di evidenziare il segmento reale CD con un colore diverso per distinguerlo dalle sue proiezioni.
Es.5
1. Disporre i 3 piani P.O., P.V. e P.L. tra di loro perpendicolari. L’asse z separa il P.V. dal P.L.;l’asse x separa il P.O. dal P.V. e corrisponde alla Linea Terra; l’asse y delimita il P.L. e il P.O. I 3 assi si intersecano nell’origine O.
2. Non è necessario calcolare la distanza del punto F dal P. O. poiché giace sul P. O., quindi spostarsi verso sinistra sulla Linea Terra di 25mm per individuare il punto F’’(distanza dal P.L.).
3. Per calcolare la distanza del punto F dal P.V. misurare 30mm sull’asse y del P.O., allontanandosi dall’origine O verso il basso.
4. Per calcolare la distanza del punto F dal P.V. si può anche centrare il compasso in O e riportare sull’asse y del P.L. la distanza di 30mm, individuando così il punto F’’’.
5. Con segno di costruzione far passare le parallele (linee di riferimento) agli assi x e y per i punti trovati nei due passaggi precedenti.
6. Queste parallele si intersecano nei punti F’. F’’ e F’’’, rispettivamente proiezione sul P.V., proiezione sul P.O. e proiezione sul P.L. I punti F’ e F’’ sono appoggiati alla Linea Terra poiché la distanza dal P.O. è 0.
7. A partire dai punti F’ e F’’’,sulla Linea Terra, riportare i segmenti E’F’=E’’’F’’’=42 verso l’alto e parallelamente all’asse z. Si individuano così i punti E’ sul P.V. ed E’’’ Sul P. L..
8. Questi due punti sono collegati da una linea di riferimento, sottile, parallela all’asse x, mentre i due segmenti E’F’ e E’’’F’’’ devono essere tracciati con linea continua evidente
9. La proiezione del segmento sul P.O. si riduce ad un punto poiché la proiezione dell’estremo E’’ coincide con l’estremo F’’. Si ricorda che si deve scrivere prima la lettera E’’ e poi F’’ perché si deve seguire l’ordine di lettura dal punto di osservazione del segmento (in questo caso dall’alto verso il basso).
Es.6
1. Disporre i 3 assi x, y e z in modo che formino 3 angoli da 120°. (Un angolo di 120° si può costruire con un angolo di 90° sommato ad un angolo di 30°).
2. Riportare lungo l’asse y, a partire da O proseguendo inclinati di 30° verso il basso a destra, la misura di 30mm (distanza dal P.V.) individuando il punto F’’’.
3. Riportare lungo l’asse x, a partire da O proseguendo inclinati di 30° verso il basso a sinistra, la misura di 25mm (distanza dal P.L.) individuando il punto F’.
4. Far passare per ognuno di questi punti, con segno di costruzione linee di riferimento), le parallele agli assi x e y.
5. Queste parallele si intersecano nel punto F’’, proiezione sul P.O.
6. Riportare lungo l’asse z, a partire da O proseguendo verso l’alto, la misura di 42mm (lunghezza del segmento EF).
7. Da questo punto sull’asse z tracciare le parallele agli assi x e y che intersecano le perpendicolari, parallele all’asse z, tracciate a partire dai punti F’ ed F’’’, nei punti E’ ed E’’’, proiezioni dell’estremo E sul P.V. e sul P.L.
8. Per trovare il punto reale E, tracciare le parallele agli assi x e y passanti per i punti E’ed E’’’.
Queste parallele si intersecano nel punto reale E.
9. Il punto reale F corrisponde alla sua proiezione sul P.O, e cioè F’’.
10. Tracciare con segno evidente colorato il segmento reale EF.
11. Tracciare in matita con segno continuo evidente i segmenti E’F’ ed E’’’F’’’. Le linee di riferimento vanno lasciate in segno continuo non evidente.
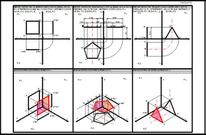
TAVOLA 16 A3 Proiezioni ortogonali di figure piane
1. Proiezione Ortogonale del quadrato ABCD (lato 30) parallelo al P.V. e perpendicolare agli altri due piani.
L’estremo C dista 12 dal P.O.; 8 dal P.L. e 25 dal P.V.
2. Assonometria Isometrica dell’esercizio 1.
3. Proiezione Ortogonale del pentagono ABCDE (lato 24) parallelo al al P.O. e perpendicolare agli altri due piani. L’estremo A dista 38 dal P.L.; 45 dal P.V. e 28 dal P.O
4. Assonometria Isometrica dell’esercizio 3.
5. Proiezione Ortogonale del triangolo equilatero ABC (lato 32) parallelo al P.L. e perpendicolare agli altri due piani. L’estremo A dista 8 dal P.V.;35 dal P.L. e 0 dal P.O.
6. Assonometria Isometrica dell’esercizio 5.
Un segmento è una parte di una retta delimitata da 2 punti, di conseguenza la sua proiezione non è altro che la congiungente delle proiezioni dei suoi due punti estremi sui piani fondamentali di proiezione.
Quando i lati dei poligoni sono inclinati rispetto ai 3 piani di proiezione, le rispettive proiezioni risultano minori della loro dimensione reale, in quanto ciascuna proiezione determina una vista scorciata (ossia il lato reale è visto da un’angolazione che ne riduce visivamente le dimensioni).
Quindi, per le Proiezioni Ortogonali, conviene sempre partire dal piano rispetto al quale il poligono è parallelo, perché solo su quel piano risulterà con le sue dimensioni reali.
Per il pentagono si parte dal P.O. dove, dopo aver collocato il punto A, si costruisce il poligono dato il lato di 24mm.
Per il triangolo equilatero si parte dal P.L. dove, dopo aver collocato il punto A, si costruisce il poligono dato il lato di 32 mm.